Spring 2017 Q7

judyohjudyoh
in W-09-RiskClassification
Screen Shot 2023-09-14 at 4.35.14 PM.png

I don't understand how off balancing works.

First of all, why are we comparing the NOMRALIZED cred-wtd ind. rel. (10) to current relativity, which looks to have its base as level A (given that level A has relativity 1.00)? Why not compare (10) to (8)?

  • As an aside, if the base is level A (again, given that level A has relativity 1.00, should we rebase the final relativities at the end of this question to level A again?) I saw a similar discussion post on this topic but I did not understand your answer.

Also, what exactly is the formula for column 12 doing and what do the values in column 12 mean? Are these relativities, but "adjusted" from the cred wtd indicated relativities so that the total can be 0? What is the final answer to this question, is it column 12?

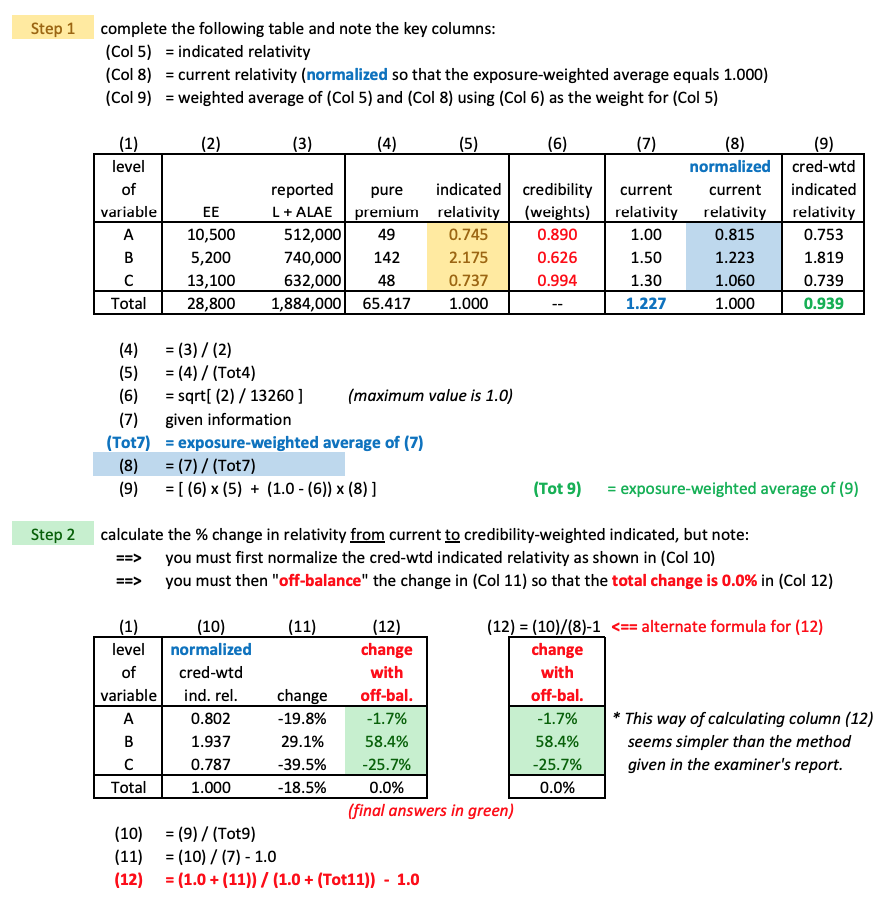
Comments

  • GrahamGraham

    A simple example that demonstrates the concept behind off-balancing is this:

    • Suppose you are doing a relativity analysis but want a revenue-neutral rate change.
    • When you calculate the new relativities, you find that the result causes a +5% overall change.
    • Since you want a revenue-neutral change, you have to reverse this 5% change on all classes. You do this by multiplying all the new relativities by the off-balance factor of 1/1.05.

    In other words, the off-balance is just a factor that is applied to all relativities to bring the overall rate change back to where you want it.

    Regarding this particular exam problem:

    • You can indeed solve it by comparing (10) to (8). That's the alternative formula for column (12) that I provided. It is mathematically equivalent.
    • You can rebase the relativities so that A is the base class but that isn't strictly necessary for this problem because the problem only asks for the changes in relativities.

    But let's rebase the relativities for illustration:

    • A becomes 0.753 / 0.753 = 1.000
    • B becomes 1.819 / 0.753 = 2.416
    • C becomes 0.739 / 0.753 = 0.981

    The exposure-weighted average of these = 1.247. Then comparing to the column (7) total, the off-balance is 1.227 / 1.247 = 0.984. If you now calculate the change in relativities using the rebased values we just calculated against the original relativities, then multiply by the off-balance of 0.983, then subtract 1.000 to get the change, you get:

    • 1.000 / 1.000 x 0.984 - 1.000 = -1.6%
    • 2.416 / 1.500 x 0.984 - 1.000 = 58.5 %
    • 0.981 / 1.300 x 0.984 - 1.000 = -25.7%

    Aside from minor rounding issues, this is the same answer as before.

Sign In or Register to comment.